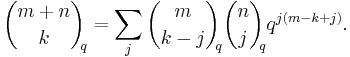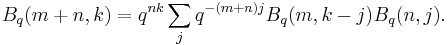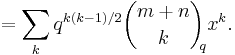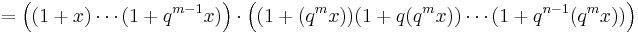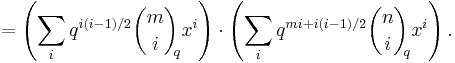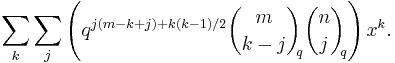q-Vandermonde identity

In mathematics, in the field of combinatorics, the q-Vandermonde identity is a q-analogue of the Chu-Vandermonde identity. Using standard notation for q-binomial coefficients, the identity states that

\binom{m %2B n}{k}_{\!\!q} = \sum_{j} \binom{m}{k - j}_{\!\!q} \binom{n}{j}_{\!\!q} q^{j(m-k%2Bj)}.

(The nonzero contributions to this sum come from values of j such that the q-binomial coefficients on the right side are nonzero, that is, 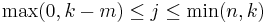\max(0, k - m) \le j \le \min(n, k).)

Contents

Other conventions

As is typical for q-analogues, the q-Vandermonde identity can be rewritten in a number of ways. In the conventions common in applications to quantum groups, a different q-binomial coefficient is used. This q-binomial coefficient, which we denote here by 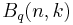B_q(n,k), is defined by 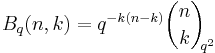B_q(n, k) = q^{-k(n-k)} \binom{n}{k}_{\!\!q^2}. (In particular, it is the unique shift of the "usual" q-binomial coefficient by a power of q such that the result is symmetric in q and 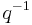q^{-1}.) Using this q-binomial coefficient, the q-Vandermonde identity can be written in the form

B_q(m %2B n,k) = q^{n k} \sum_{j} q^{-(m%2Bn)j} B_q(m,k - j) B_q(n,j). \,

Proofs of the identity

As with the (non-q) Chu-Vandermonde identity, there are several possible proofs of the q-Vandermonde identity. We give one proof here, using the q-binomial theorem.

One standard proof of the Chu-Vandermonde identity is to expand the product 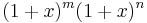(1 %2B x)^m (1 %2B x)^n in two different ways. Following Stanley,[1] we can tweak this proof to prove the q-Vandermonde identity, as well. First, observe that the product

(1 %2B x)(1 %2B qx) \cdots (1 %2B q^{m %2B n - 1}x)

can be expanded by the q-binomial theorem as

(1 %2B x)(1 %2B qx) \cdots (1 %2B q^{m %2B n - 1}x)
= \sum_k q^{k(k-1)/2} \binom{m %2B n}{k}_{\!\!q} x^k.

Less obviously, we can write

(1 %2B x)(1 %2B qx) \cdots (1 %2B q^{m %2B n - 1}x)
= \left((1 %2B x)\cdots (1 %2B q^{m - 1}x)\right) \cdot \left((1 %2B (q^m x))(1 %2B q(q^m x)) \cdots (1 %2B q^{n - 1}(q^m x))\right)

and we may expand both subproducts separately using the q-binomial theorem. This yields

(1 %2B x)(1 %2B qx) \cdots (1 %2B q^{m %2B n - 1}x)
= \left(\sum_i q^{i(i - 1)/2} \binom{m}{i}_{\!\!q} x^i \right) \cdot \left(\sum_i q^{mi %2B i(i - 1)/2} \binom{n}{i}_{\!\!q} x^i \right).

Multiplying this latter product out and combining like terms gives

\sum_k \sum_j \left(q^{j(m - k %2B j) %2B k(k - 1)/2} \binom{m}{k - j}_{\!\!q} \binom{n}{j}_{\!\!q}\right)x^k.

Finally, equating powers of x between the two expressions yields the desired result.

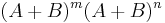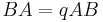This argument may also be phrased in terms of expanding the product (A %2B B)^m(A %2B B)^n in two different ways, where A and B are operators (for example, a pair of matrices) that "q-commute," that is, that satisfy BA = q AB.

Proof by counting subspaces

Notes

  1. ^ Stanley (2011), Solution to exercise 1.100, p. 188.

References